Sampling with uniform probability is easy. Let's say you have a list of numbers, [1, 2, 3, 4, 5]. If you give each one equal probability of 0.20, then you can use a (psuedo) random number generator to select entries from the list. What if you want, say, 1 to be more likely? Maybe you add an extra 1 to the list: [1, 1, 2, 3, 4, 5]. Or as many 1s as you need. For discrete distributions, it's pretty easy to obtain a simple random sample.
For continuous distributions, it gets harder. First, there are infinite numbers you can pick from. Maybe you want to sample in an interval [0, 1], but you want numbers around 0.4 or so to be more likely. How do you define the probabilities of each number? What do I even mean by each number? 0.0000001, 0.000002? But what about 0.000000001? With a discrete distribution you can use a histogram, get a total count, divide by the total count to get a probability, etc. But how do you sample from something like this?
Continuous Probability Distributions
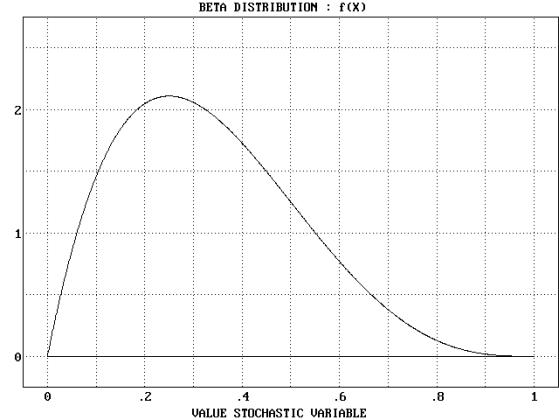
The curve above is a kind of probability distribution, specifically a Beta distribution. The x axis are the numbers that the distribution takes on, and the y axis is the probability density. The probability density is just a relative indicator of how likely a particular x value is. It's set the way it is because all probability distributions have to integrate to 1. If the curve above was even more concentrated at say 0.25, then the probability density would be higher at that point while lower at other points, to show that it's relatively more likely.
Rejection sampling
One naive and intuitive way to randomly sample from a continuous distribution, is by rejection sampling. To start, what do we know, and what can we do that's easy? We know the x value interval we want to sample between. We also should know some high bound of the function - it's possible that the high bound is huge, but we should be able to roughly graph the distribution and then figure a safe upper bound.
We want to draw samples that are representative of the "target" distribution, so we can't just pick uniform x values. Uniform x values would give us a graph, and we want a random sample. Nor can we pick uniform y values, because whether they are valid y values depends on the x value they're associated with.
So, we'll uniformly pick random x and y values, together.
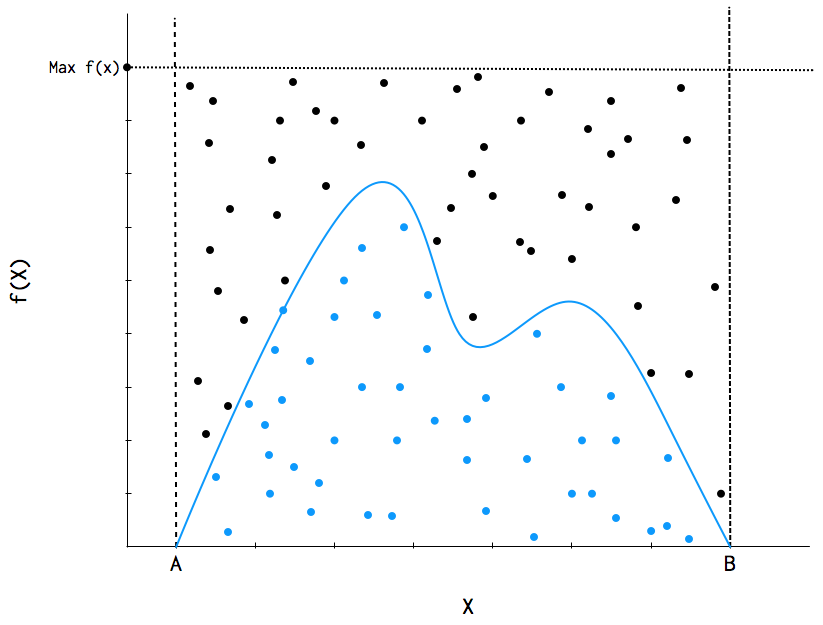
The blue curve is the distribution we want. We don't know how to sample from it, but we know samples from it are going to be from under that black line labeled Max f(x). All the points on the distribution are different random x and y values we generated. Let's look at one case - let's say one point has x = a and y = b, and the curve function is given by f. Then, to decide whether to "accept" or "reject" (a, b), we evaluate f(a), and if f(a) > b, we accept, otherwise we reject. Intuitively, we say that if the point has a y value less than or equal to the curve (is below the curve), then we take it. This will give us the points that lie under the curve, the blue points in the graph above. Since the density of the curve is lower in certain areas, more points will be rejected there. The more points we take, the better the resulting density of our sample matches the density of our target distribution.
Weaknesses
- Rejection sampling can get pretty slow if the bound doesn't fit the distribution well.
- Rejection sampling can get pretty slow if the target distribution is high dimensional.
- Rejection sampling can get pretty slow if the target distribution is uneven.
Mitigating Weaknesses
- Imagine if we fit a normal distribution instead of a uniform one as the upper bound? For that matter, we could choose any easily-samplable distribution as the upper bound, as long as it's above the target distribution at every possible x.
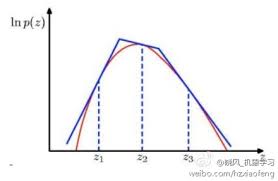
- In fact, for log-concave densities (they look round and slope down like a hill), we can use a technique called adaptive rejection sampling which basically drapes lines over the hill. The best part is that when we reject a point, we can fold the tent in a little tighter. The downside is that this usually doesn't work with high dimensions.
Code
Here's a sample implementation in R:
rejectionSample = function (n, f, x.interval = c(0, 1), upper.bound = function (x) { 10 }) {
# n is the number of points wanted
# f is the target distribution
# x.interval is the A,B range of x values possible.
# upper.bound is the high bound of the rejection sampler. Notice
# that the input is a function so you can use a rnorm or something if you'd like.
pts = vector("numeric", n) # This vector will hold our points.
ix = 1 # This is our current position in the pts array
while (ix < n) {
x = runif(1, x.interval[1], x.interval[2]) # Take a random x value.
y = runif(1, 0, upper.bound(x)) # Take a random y value
if (f(x) >= y) {
pts[ix] = x
ix = ix + 1
}
}
return(pts)
}
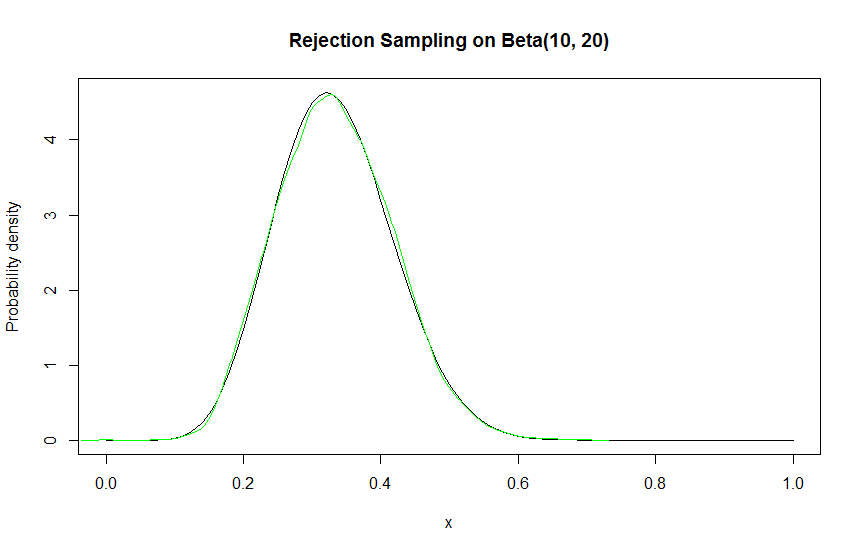
target = function (x) { dbeta(x, 10, 20) }
points = rejectionSample(n = 10000, target, upper.bound = function (x) { 6 })
curve(target, from = 0, to = 1)
lines(density(points), col="green")